Ôn tập chương Hàm số và đồ thị

a)2 đại lượng y và x tỉ lệ thuận với nhau khi đại lượng x liên hệ với đại lượng y theo công thức y=ax ( a là hằng số khác 0)

VD:6 và 3 tỉ lệ thuận với nhau theo công thức 6=2.3

b)2 đại lượng y và x tỉ lệ nghịch với nhau khi đại lượng x liên hệ với đại lượng y theo công thức xy=a hay \(\dfrac{a}{x}=y\) ( a là hằng số khác 0)

VD: 6 và 3 tỉ lệ nghịch với nhau theo công thức 6.3=18

a)Hai đại lượng y và x tỉ lệ thuận với nhau khi đại lượng x liên hệ với đại lượng y theo công thức y=a\(\cdot\)x(a\(\ne\)0;a là hằng số)

VD:6vaf 3 tỉ lệ với nhau theo công thức 6=2\(\cdot\)3

b)Hai đại lượng y và x tỉ lệ nghịch với nhau khi 2đại lượng x,y liên hệ với nhau theo công thức xy=a hay \(\dfrac{a}{x}=y\)(a là hằng số khác 0)

VD: 6 và 3 tỉ lệ nghịch với nhau theo công thức 6,3=18

nhầm:6.3=18

x là cạnh tam giác đều, y là chu vi tam giác đều

\(\Rightarrow y=3x\)

Vậy y tỉ lệ thuận với x

Chu vi của tam giác đều là y = x+x+x=3x.

Với công thức y=3x chứng tỏ rằng đại lượng y tỉ lệ thuận với đại lượng x.

Sách Giáo Khoa:

+ Tỉ lệ thuận có nghĩa là đại lượng x tăng thì đại lượng y cũng tăng

+Tỉ lệ nghịch có nghĩa là đại lượng x tăng thì đại lượng y giảm và ngược lại, đại lượng y tăng thì đại lượng y giảm

=>trong trường hợp này thì x và y tỉ lệ nghịch với nhau

Ta biết thể tích hình hộp chữ nhật bằng diện tích đáy nhân với chiều cao.

Theo đề bài ta có : 36= y.x \(\Rightarrow y=\dfrac{36}{x}\)

Với công thức này chứng tỏ rằng đại lượng y tỉ lệ nghịch với đại lượng x.

theo đề bài ta có y.x=36(cm³)

Vậy y tỉ lệ nghịch với x

Đồ thị của hàm số \(y=ax\);( \(a\ne0\)) là một đường thẳng đi qua gốc tọa độ.

Đồ thị của hàm số y = a x ; ( a ≠ 0 ) là một đường thẳng đi qua gốc tọa độ

Đồ thị của hàm số y = ax (a khác 0) là 1 đường thẳng đi qua gốc tọa độ và 1 (hoặc nhiều) điểm thuộc đồ thị hàm số đó.

Đổi 1 tấn = 1000000 gam;

25kg = 25000 gam

Gọi x là lượng muối có trong 250g nước biển

Vì lượng nước biển và lượng muối chứa trong đó là hai đại lượng tỉ lệ thuận nên ta có: 1000000/25000 = 250/x

⇒ x = 25000.250/1000000 = 6,25

Vạy trong 250g nước biển chứ 6.25g muối.

Bài giải: Đổi 1 tấn = 1000000 gam; 25kg = 25000 gam

Gọi x là lượng muối có trong 250g nước biển Vì lượng nước biển và lượng muối chứa trong đó là hai đại lượng tỉ lệ thuận nên ta có:

1000000/25000 = 250/x

⇒ x = 25000.250/1000000 = 6,25

Vậy trong 250g nước biển chứa 6.25g muối.

Đổi đơn vị: Đổi cùng đơn vị đo là gam.

Ta có: 1 tấn = 1000000g

25kg = 25000g

Gọi lượng muối trong 250g nước biển là x. Vì lượng nước biển và lượng nước muối chứa trong đó là hai đại lượng tỉ lệ thuận nên theo tính chất của đại lượng tỉ lệ thuận ta có :

\(\dfrac{250}{x}=\dfrac{1000000}{25000}=40\Rightarrow x=\dfrac{250}{40}=6,25\left(g\right)\)

Vậy 250 gam nước biển chứa 6,25g muối.

Ta biết rằng công thức tình khối lượng của thanh kim loại đồng chất được tính theo công thức : \(\left\{{}\begin{matrix}m:g\\V:cm^3\\D:\dfrac{g}{cm^3}\end{matrix}\right.\)

Gỉa sử với thanh sắt ,ta có:m =D.V= 7,8.V

và thanh chì , ta có:\(m^,=D^,.V^,=11,3V^,\)

Vì m = \(m^,\) nên 7,8V = 11,3\(V^,\)

\(\Rightarrow\)\(\dfrac{V}{V^,}=\dfrac{11,3}{7,8}\approx1,45\)

Vậy thanh sắt có thể tích lớn hơn và lớn hơn 1,45 lần so với thể tích thanh chì.

Vì m = V.D và m là hằng số có khối lượng bằng nhau nên V và D là hai đại lượng tỉ lệ nghịch với nhau với hệ số tỉ lệ dương.

Theo tính chất đại lượng tỉ lệ nghịch với nhau với hệ số tỉ lệ dương. Theo tính chất của đại lượng tỉ lệ nghịch, ta có:

Vậy thể tích thanh sắt lớn hơn và lớn hơn khoảng 1,45 lần.

Hướng dẫn:

Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB

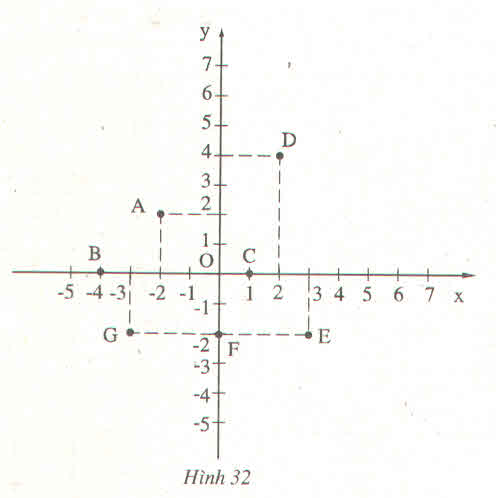
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)

Tam giác ABC là tam giác vuông tại B.

Hướng dẫn làm bài:

Ta có quãng đường đi được và thời gian là hai đại lượng tỉ lệ thuận.

Ta có công thức: S = 35.t

Với t = 1 =>S= 35 ta được A(1;35) thuộc đồ thị.

Với S = 140 => \(\Rightarrow t = {{140} \over {35}} = 4\) ta được B (4;140) thuộc đồ thị.

Ta được đồ thị chuyển động là đoạn thẳng OB như trên hình vẽ.