Trong hai mệnh đề sau đây, mệnh đề nào đúng ? Mệnh đề nào sai ?
a) Hai tam giác bằng nhau thì đồng dạng với nhau
b) Hai tam giác đồng dạng với nhau thì bằng nhau

Trong hai mệnh đề sau đây, mệnh đề nào đúng ? Mệnh đề nào sai ?
a) Hai tam giác bằng nhau thì đồng dạng với nhau
b) Hai tam giác đồng dạng với nhau thì bằng nhau


Giải:
∆A'B'C' ∽ ∆A"B"C" theo tỉ số đồng dạng K1 =
∆A"B"C" ∽∆ ABC theo tỉ số đồng dạng k2 =
Theo tính chất 3 thì ∆A'B'C' ∽ ∆ABC.
Theo tỉ số K= = = .
vậy K= K1.k2

Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số \(\dfrac{1}{2}\)
Lấy trung điểm M của AB, N là trung điểm của AC => MN là đường trung bình của tam giác ABC.
=> MN // BC.
=> ∆ AMN ∽ ∆ABC theo tỉ số K = 1/2.

Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ lệ đồng dạng \(k=\dfrac{2}{3}\)
Giải:
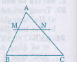
Trên cạnh AB lấy điểm M sao cho AM= AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)

Từ điểm M thuộc cạnh AB của tam giác ABC với \(AM=\dfrac{1}{2}MB\), kẻ các tia song song với AC và BC, chúng cắt BC và AC lần lượt tại L và N
a) Nêu tất cả các cặp tam giác đồng dạng
b) Đối với mỗi cặp tam giác đồng dạng, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng
a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC
và ∆AMN ∽ ∆MLB
b)
∆AMN ∽ ∆ABC có:
= ; =
=
∆MBL ∽ ∆ABC có:
= , chung, =
=
∆AMN ∽ ∆MLB có:
= , = , =


a) Theo bài ra ta có;
∆A'B'C' ∽ ∆ABC theo tỉ số đồng dạng K= .
=> =
=
=
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
=> =
=
=
Vậy tỉ số chu vi của ∆A'B'C' và ∆ABC là .
b) Vì =
mà
-
= 40dm
=> =
=
= 20
=> = 100 dm
= 60 dm

Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng k ?



Tam giác ABC có AB = 3cm, BC = 5cm và CA = 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5 cm.
Tính các cạnh còn lại của tam giác A'B'C' ?


Cho tam giác ABC có AB = 16,2 cm, BC = 24,3 cm; AC = 32,7 cm. Tính độ dài các cạnh của tam giác A'B'C', biết rằng A'B'C' đồng dạng với tam giác ABC và
a) A'B' lớn hơn cạnh AB là 10,8 cm
b) A'B' bé hơn cạnh AB là 5,4 cm


Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
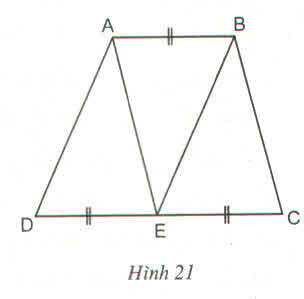
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)

a) a là mệnh đề đúng.
b) b là mệnh đề sai