Giải các phương trình sau :
a) \(\sin\left(x+2\right)=\dfrac{1}{3}\)
b) \(\sin3x=1\)
c) \(\sin\left(\dfrac{2x}{3}-\dfrac{\pi}{3}\right)=0\)
d) \(\sin\left(2x+20^0\right)=-\dfrac{\sqrt{3}}{2}\)
Với những giá trị nào của x thì giá trị của các hàm số \(y=\sin3x;y=\sin x\) bằng nhau ?
Bài 2. x thỏa mãn yêu cầu bài ra khi và chỉ khi
.png)
Giải các phương trình sau :
a) \(\cos\left(x-1\right)=\dfrac{2}{3}\)
b) \(\cos3x=\cos12^0\)
c) \(\cos\left(\dfrac{3x}{2}-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
d) \(\cos^22x=\dfrac{1}{4}\)
Bài 3. a) cos (x - 1) = .png)
⇔ x - 1 = ±arccos + k2π
⇔ x = 1 ±arccos + k2π , (k ∈ Z).
b) cos 3x = cos 120 ⇔ 3x = ±120 + k3600 ⇔ x = ±40 + k1200 , (k ∈ Z).
c) Vì .png)
= cos.png)
nên .png)
⇔ cos(.png)
) = cos ⇔ = ± + k2π ⇔
.png)
d) Sử dụng công thức hạ bậc .png)
(suy ra trực tiếp từ công thức nhan đôi) ta có
.png)
⇔ .png)
⇔ .png)
⇔ .png)
⇔ .png)
Giải phương trình :
\(\dfrac{2\cos2x}{1-\sin2x}=0\)
Đáp án :
Bài 4. Ta có
.png)
= 0 ⇔ .png)
⇔ sin2x = -1 ⇔ 2x = .png)
+ k2π ⇔ x = .png)
+ kπ, (k ∈ Z).
Giải các phương trình sau :
a) \(\tan\left(x-15^0\right)=\dfrac{\sqrt{3}}{3}\)
b) \(\cot\left(3x-1\right)=-\sqrt{3}\)
c) \(\cos2x\tan x=0\)
d) \(\sin3x\cot x=0\)
Bài 5. a) Vì .png)
= tan 300 nên
tan (x - 150) = ⇔ tan (x - 150) = tan 300
⇔ x - 150 = 300 + k1800 ⇔ x = 450 + k1800 , (k ∈ Z).
b) Vì -√3 = cot(.png)
) nên
cot (3x - 1) = -√3 ⇔ cot (3x - 1) = cot()
⇔ 3x - 1 = + kπ ⇔ x = .png)
c) Đặt t = tan x thì cos2x = .png)
, phương trình đã cho trở thành
. t = 0 ⇔ t ∈ {0 ; 1 ; -1} .
Vì vậy phương trình đã cho tương đương với
.png)
d) sin 3x . cot x = 0 ⇔ .png)
.
Với điều kiện sinx # 0, phương trình tương đương với
sin 3x . cot x = 0 ⇔ .png)
Với cos x = 0 ⇔ x = .png)
+ kπ, k ∈ Z thì sin2x = 1 – cos2x = 1 – 0 = 1 => sinx # 0, điều kiện được thỏa mãn.
Với sin 3x = 0 ⇔ 3x = kπ ⇔ x = .png)
, (k ∈ Z). Ta còn phải tìm các k nguyên để x = vi phạm điều kiện (để loại bỏ), tức là phải tìm k nguyên sao cho sin = 0, giải phương trình này (với ẩn k nguyên), ta có
sin = 0 ⇔ = lπ, (l ∈ Z) ⇔ k = 3l ⇔ k : 3.
Do đó phương trình đã cho có nghiệm là x = + kπ, (k ∈ Z) và x = (với k nguyên không chia hết cho 3).
Với những giá trị nào của x thì giá trị của các hàm số \(y=\tan\left(\dfrac{\pi}{4}-x\right)\) và \(y=\tan2x\) bằng nhau ?
Bài 6. Các giá trị cần tìm của x là các nghiệm của phương trình
tan 2x = tan (.png)
- x) ,
Đáp số : 
( k ∈ Z, k - 2 không chia hết cho 3).
Giải các phương trình sau :
a) \(\sin3x-\cos5x=0\)
b) \(\tan3x.\tan x=1\)
Bài 7. a) sin 3x - cos 5x = 0 ⇔ cos 5x = sin 3x ⇔ cos 5x = cos (
- 3x) ⇔
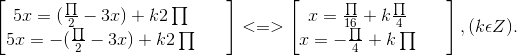
b) tan 3x . tan x = 1 ⇔ 
. Điều kiện : cos 3x . cos x # 0.
Với điều kiện này phương trình tương đương với
cos 3x . cos x = sin 3x . sinx ⇔ cos 3x . cos x - sin 3x . sinx = 0 ⇔ cos 4x = 0.
Do đó
tan 3x . tan x = 1 ⇔ 
⇔ cos 2x = 
⇔ cos 4x = 0
⇔ 
Giải các phương trình :
a) \(\sin3x=-\dfrac{\sqrt{3}}{2}\)
b) \(\sin\left(2x-15^0\right)=\dfrac{\sqrt{2}}{2}\)
c) \(\sin\left(\dfrac{x}{2}+10^0\right)=-\dfrac{1}{2}\)
d) \(\sin4x=\dfrac{2}{3}\)
Giải các phương trình :
a) \(\cos\left(x+3\right)=\dfrac{1}{3}\)
b) \(\cos\left(3x-45^0\right)=\dfrac{\sqrt{3}}{2}\)
c) \(\cos\left(2x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
d) \(\left(2+\cos x\right)\left(3\cos2x-1\right)=0\)
Giải các phương trình :
a) \(\tan\left(2x+45^0\right)=-1\)
b) \(\cot\left(x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
c) \(\tan\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)=\tan\dfrac{\pi}{8}\)
d) \(\cot\left(\dfrac{x}{3}+20^0\right)=-\dfrac{\sqrt{3}}{3}\)
a) \(x=-45^0+k90^0,k\in\mathbb{Z}\)
b) \(x=-\dfrac{\pi}{6}+k\pi,k\in\mathbb{Z}\)
c) \(x=\dfrac{3\pi}{4}+k2\pi,k\in\mathbb{Z}\)
d) \(x=300^0+k540^0,k\in\mathbb{Z}\)
Bài 1. a) sin (x + 2) =.png)
⇔ .png)
⇔.png)
b) sin 3x = 1 ⇔ 3x =.png)
+ k2π ⇔ x = .png)
, (k ∈ Z).
c) sin (.png)
) = 0 ⇔ .png)
= kπ ⇔ x = .png)
, (k ∈ Z).
d) Vì.png)
= sin(-600) nên phương trình đã cho tương đương với
sin (2x +200) = sin(-600)
⇔.png)
⇔.png)