Giúp mik với!!
Toán
Mọi người giúp em câu 5c với ạ, em cảm ơn
Bài 2 : Cho đường tròn (0) Có đường kính AB vuông góc với dây cung MN tại H(H năm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (0) sao cho đoạn tháng AC cắt đường tròn (0) tại điểm K khác A, hai dây MN và BK cắt nhau ở E.
a) Chứng minh rằng: Tứ giác AHEK là tứ giác nội tiếp
b) Chứng minh rằng: △ CHACKE, từ đó suy ra CH. KE = AH . CK
c) Chứng minh: MB = NB.
Cho A=6n/3n+1 tìm giá trị của n để A là một số nguyên
ĐKXĐ: n<>-1/3
Để A là số nguyên thì \(6n⋮3n+1\)
=>\(6n+2-2⋮3n+1\)
=>\(-2⋮3n+1\)
=>\(3n+1\in\left\{1;-1;2;-2\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1\right\}\)
Đúng 0
Bình luận (0)
Để \( A \) là một số nguyên, ta cần tìm giá trị của \( n \) sao cho phần tử số hạng của \( A \) là một số nguyên. Điều này đồng nghĩa với việc \( 6n \) chia hết cho \( 3n + 1 \) mà không dư.
Ta có thể viết phương trình này dưới dạng:
\[ \frac{6n}{3n + 1} = k \]
Trong đó \( k \) là một số nguyên dương.
Để giải phương trình này, chúng ta có thể nhân cả hai vế của phương trình với \( 3n + 1 \), ta được:
\[ 6n = k(3n + 1) \]
Mở ngoặc:
\[ 6n = 3kn + k \]
\[ 6n - 3kn = k \]
\[ n(6 - 3k) = k \]
\[ n = \frac{k}{6 - 3k} \]
Để \( n \) là một số nguyên dương, \( k \) phải là một ước số của 6-3k.
Ta sẽ kiểm tra các giá trị của \( k \) từ 1 đến 6, vì \( k \) là một ước số của 6-3k:
1. Khi \( k = 1 \): \( 6 - 3 \times 1 = 3 \), 6 không chia hết cho 3, không thỏa mãn.
2. Khi \( k = 2 \): \( 6 - 3 \times 2 = 0 \), không hợp lệ vì chia cho 0.
3. Khi \( k = 3 \): \( 6 - 3 \times 3 = -3 \), không phải số nguyên dương.
4. Khi \( k = 4 \): \( 6 - 3 \times 4 = -6 \), không phải số nguyên dương.
5. Khi \( k = 5 \): \( 6 - 3 \times 5 = -9 \), không phải số nguyên dương.
6. Khi \( k = 6 \): \( 6 - 3 \times 6 = -12 \), không phải số nguyên dương.
Không có giá trị của \( k \) nào làm cho \( n \) là một số nguyên dương. Điều này ngụ ý rằng không có giá trị của \( n \) nào thỏa mãn điều kiện để \( A \) là một số nguyên.
Đúng 1
Bình luận (0)

cho mik xin hình với ạ
Cho tam giác ABC vuông tại A (AB<AC), kẻ đường cao AH và đường trung tuyến AM (H,M thuộc BC). Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng min rằng :
a) DE2 = BH.HC
b) AH2=AD.DB+AE.EC
c) DE vuông góc với AM
a: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>DE=AH
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC=DE^2\)
b: Xét ΔDHA vuông tại D và ΔDBH vuông tại D có
\(\widehat{DHA}=\widehat{DBH}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔDHA~ΔDBH
=>\(\dfrac{DH}{DB}=\dfrac{DA}{DH}\)
=>\(DH^2=DA\cdot DB\)
Xét ΔEAH vuông tại E và ΔEHC vuông tại E có
\(\widehat{EAH}=\widehat{EHC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔEAH~ΔEHC
=>\(\dfrac{EA}{EH}=\dfrac{EH}{EC}\)
=>\(EH^2=EA\cdot EC\)
ADHE là hình chữ nhật
=>\(DE^2=HD^2+HE^2\)
=>\(AH^2=AD\cdot DB+AE\cdot EC\)
c: ΔBAC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)
Ta có:ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{B}\)
\(\widehat{AED}+\widehat{MAC}=\widehat{B}+\widehat{C}=90^0\)
=>DE\(\perp\)AM
Đúng 0
Bình luận (0)
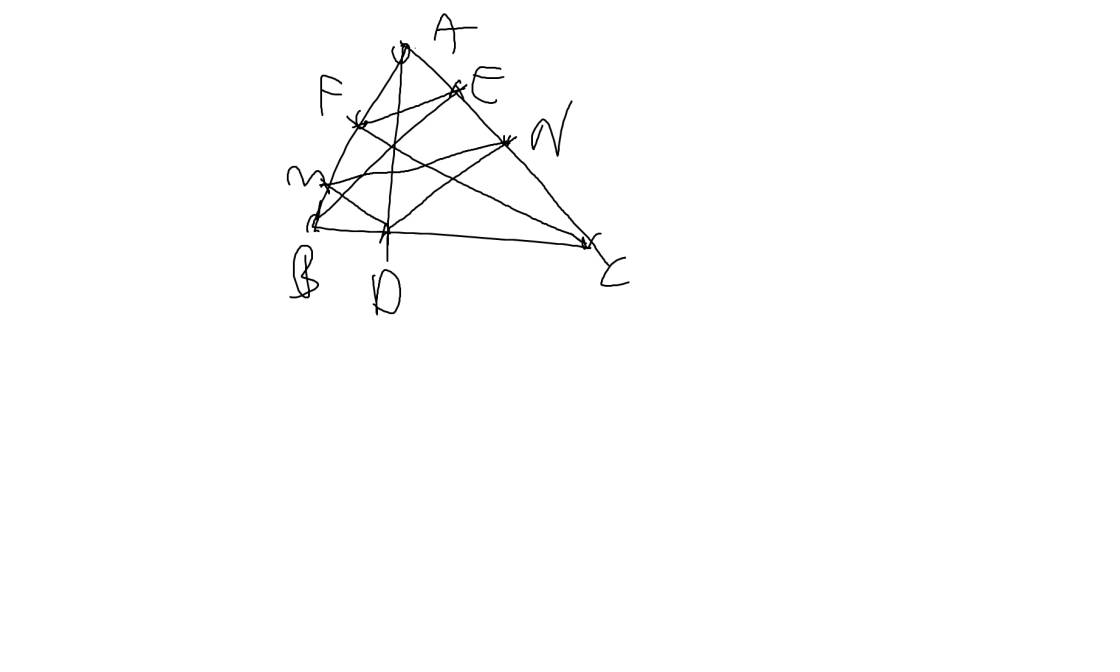
Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song son vớ đáy AB cắt các cạnh bên AD,BC theo thứ tự ở M và N.
a) Chứng minh : OA.BD=OB.AC
b) Chứng minh OM=ON
Tham khảo:
a) Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \(AB\). Khi đó, ta có hai tam giác vuông \(OAH\) và \(OBH\).
Trong tam giác \(OAH\), ta có:
\[\frac{OA}{AH} = \frac{OD}{BD} \quad (1)\]
Trong tam giác \(OBH\), ta có:
\[\frac{OB}{BH} = \frac{OC}{AC} \quad (2)\]
Nhân cả hai phương trình (1) và (2), ta được:
\[\frac{OA}{AH} \times \frac{OB}{BH} = \frac{OD}{BD} \times \frac{OC}{AC}\]
\[OA \times OB = \frac{AH \times BH \times OD \times OC}{BD \times AC}\]
Do đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\), nên \(AH \times BH = OH^2\) (vì \(OH\) là đường cao của tam giác \(OAB\)), \(OD \times OC = OD \times OC\) (vì \(OD\) và \(OC\) là đường cao của tam giác \(OCD\)), nên:
\[OA \times OB = \frac{OH^2 \times OD \times OC}{BD \times AC}\]
\[OA \times OB = \frac{OD \times OC \times OH^2}{BD \times AC}\]
Nhưng ta biết rằng \(OH^2 = OA \times OB\), từ đó suy ra \(OA \times OB = OA \times OB\).
Vậy, \(OA \times OB = OA \times OB\), điều này đã được chứng minh.
b) Ta có thể sử dụng định lí hình chiếu góc bằng nhau để chứng minh rằng \(OM = ON\). Cụ thể, ta có hai tam giác vuông \(OAM\) và \(OBN\) có:
\[\angle OAM = \angle OBN\]
\[\angle AOM = \angle BON = 90^\circ\]
Vì vậy, các tam giác \(OAM\) và \(OBN\) đồng dạng theo góc và cạnh nên \(OM = ON\).
Đúng 0
Bình luận (0)
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB~ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(AC\cdot OB=AO\cdot BD\)
b: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BO}{BD}\left(2\right)\)
Ta có: \(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{AO}{AC}=\dfrac{OB}{BD}\left(3\right)\)
Từ (3),(2),(1) suy ra OM=ON
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (ACAB). Vẽ đường cao AH(H thuộc BC). Trên tia đối của tia BC lấy điểm K sao cho KHHA. Qua K kẻ đường thẳng song song với AH, cắt đường thẳng AC tại P.a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC.b) Chứng minh CB.CKCA.CP và tam giác CAK đồng dạng với tam giác CBP.c) Gọi Q là trung điểm của BP. Chứng minh : QH là đường trung trực của đoạn thẳng AK.
Đọc tiếp
Cho tam giác ABC vuông tại A (AC>AB). Vẽ đường cao AH(H thuộc BC). Trên tia đối của tia BC lấy điểm K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH, cắt đường thẳng AC tại P.
a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC.
b) Chứng minh CB.CK=CA.CP và tam giác CAK đồng dạng với tam giác CBP.
c) Gọi Q là trung điểm của BP. Chứng minh : QH là đường trung trực của đoạn thẳng AK.
Tham khảo
a) Ta có:
\[\angle CKP = \angle CAH = 90^\circ \] (vì AH là đường cao của tam giác ABC)
\[ \angle KCP = \angle KAH \] (vì CP song song với AH)
\[ KP = AH \] (theo định lí về đường cao trong tam giác vuông)
\[ KC = KH \] (vì \( KH = AH \))
Do đó, tam giác \(KPC\) đồng dạng với tam giác \(AHC\) (cùng có một góc vuông, và góc tại \(K\) bằng góc tại \(A\)).
b) Từ phần a), ta biết \(KC = AH\) và \(CP = KH\).
\[ \frac{CK}{AH} = \frac{CP}{KH} \]
\[ \frac{CK}{AC} = \frac{CP}{CP + PH} \]
\[ CK \times CP + CK \times PH = AC \times CP \]
\[ CK \times CP + AH \times PH = AC \times CP \]
\[ CP \times (CK + PH) = AC \times CP \]
\[ CK + PH = AC \]
Vậy \(CB \times CK = CA \times CP \).
Từ phần a), tam giác \(KPC\) đồng dạng với tam giác \(AHC\), nên \(\frac{CK}{AC} = \frac{AH}{AB}\).
\[ CK = \frac{AC \times AH}{AB} \]
\(AH\) là đường cao của tam giác ABC, nên \(AH = \frac{AB \times AC}{BC}\).
\[ CK = \frac{AC^2}{BC} \]
Tương tự,
\[ CP = \frac{AC^2}{BC + AC} \]
\[ CB \times CK = CA \times CP \]
Ta chứng minh được \(CB \times CK = CA \times CP \).
Ta có:
\[\angle CAK = \angle CBP = 90^\circ \] (vì \(AK \parallel CP\), cả hai đường thẳng đều vuông góc với AC)
\[ \angle CKA = \angle BCP \] (vì \(CK \parallel AB\))
\[ AK = BP \] (vì \(AK \parallel BP\) và \(AK = BP = \frac{1}{2} BC\) - đường trung bình của tam giác \(ABC\))
Do đó, tam giác \(CAK\) đồng dạng với tam giác \(CBP\).
c) Gọi \(Q\) là trung điểm của \(BP\).
\[ \frac{PH}{CP} = \frac{1}{2} \]
\[ PH = \frac{1}{2} CP \]
\(K\) là điểm trên tia đối của \(BC\) sao cho \(KH = AH\), nên \(KH = \frac{1}{2} BC\).
\[ AK = \frac{1}{2} BC \]
Vậy, \(QH\) là đoạn thẳng cắt đôi \(AK\).
Đúng 0
Bình luận (0)
a: Ta có: AH\(\perp\)BC
KP//AH
Do đó: KP\(\perp\)BC
Xét ΔACB vuông tại A và ΔKCP vuông tại K có
\(\widehat{ACB}\) chung
Do đó: ΔACB~ΔKCP
b: ΔACB~ΔKCP
=>\(\dfrac{CA}{CK}=\dfrac{CB}{CP}\)
=>\(\dfrac{CA}{CB}=\dfrac{CK}{CP}\)
=>\(CA\cdot CP=CK\cdot CB\)
Xét ΔCAK và ΔCBP có
\(\dfrac{CA}{CB}=\dfrac{CK}{CP}\)
\(\widehat{ACK}\) chung
Do đó: ΔCAK~ΔCBP
c: ΔBAP vuông tại A
mà AQ là đường trung tuyến
nên \(AQ=\dfrac{BP}{2}\left(1\right)\)
Ta có: ΔKPB vuông tại K
mà KQ là đường trung tuyến
nên \(KQ=\dfrac{BP}{2}\left(2\right)\)
Từ (1),(2) suy ra QA=QK
=>Q nằm trên đường trung trực của AK(3)
Ta có: HA=HK
=>H nằm trên đường trung trực của AK(4)
Từ (3),(4) suy ra QH là đường trung trực của AK
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn đường cao AD BE CF cắt nhau tại H .Chứng minh Tam giác HFB đồng dạng với tam giác HEC chứng minh BH.BE=BD.BC Chứng minh BH.BE + CH.CF =BC^2
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)
Do đó: ΔFHB\(\sim\)ΔEHC
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{DBH}\) chung
Do đó: ΔBDH\(\sim\)ΔBEC
Suy ra: BD/BE=BH/BC
hay \(BD\cdot BC=BE\cdot BH\)
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)
Do đó: ΔFHB\(\sim\)ΔEHC
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{DBH}\) chung
Do đó: ΔBDH\(\sim\)ΔBEC
Suy ra: BD/BE=BH/BC
hay \(BD\cdot BC=BE\cdot BH\)
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
\(\widehat{DCH}\) chung
Do đó: ΔCDH~ΔCFB
=>\(\dfrac{CD}{CF}=\dfrac{CH}{CB}\)
=>\(CD\cdot CB=CH\cdot CF\)
\(BH\cdot BE+CH\cdot CF\)
\(=BD\cdot BC+CD\cdot BC=BC\left(BD+CD\right)=BC^2\)
Đúng 0
Bình luận (0)