Bài 2: Quy tắc tính đạo hàm
Nội dung lý thuyết
Các phiên bản khácI. ĐẠO HÀM CỦA MỘT HÀM SỐ THƯỜNG GẶP
- Định lí 1:
Hàm số \(y=x^n\) (\(n\in N,n>1\)) có đạo hàm tại mọi \(x\in R\) và
\(\left(x^n\right)'=nx^{n-1}\).
Ví dụ: \(\left(x^2\right)'=2x\)
Nhận xét: +) Đạo hàm của hàm hằng bằng 0 : \(\left(c\right)'=0\)
+) Đạo hàm của hàm số \(y=x\) bằng 1 : \(\left(x\right)'=1\)
- Định lí 2:
Hàm số \(y=\sqrt{x}\) có đạo hàm tại mọi \(x\) dương và
\(\left(\sqrt{x}\right)'=\dfrac{1}{2\sqrt{x}}\).
II. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG
1. Định lí
- Định lí 3:
Giả sử \(u=u\left(x\right)\), \(v=v\left(x\right)\) là các hàm số có đạo hàm tại điểm \(x\) thuộc khoảng xác định. Ta có:
\(\left(u+v\right)'=u'+v'\)
\(\left(u-v\right)'=u'-v'\)
\(\left(uv\right)'=u'v+uv'\)
\(\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}\left(v=v\left(x\right)\ne0\right)\).
Ví dụ 1: Tính đạo hàm của hàm số \(y=x^2-x^4+\sqrt{x}\).
Giải:
Ta có: \(y'=(x^2-x^4+\sqrt{x})'=2x-4x^3+\dfrac{1}{2\sqrt{x}}\).
Ví dụ 2: Tính đạo hàm của hàm số \(y=x^3\left(\sqrt{x}-x^5\right)\).
Giải:
Ta có: \(y'=[x^3\left(\sqrt{x}-x^5\right)]'=\left(x^3\right)'\left(\sqrt{x}-x^5\right)+x^3\left(\sqrt{x}-x^5\right)'\)
\(=3x^2\left(\sqrt{x}-x^5\right)+x^3\left(\dfrac{1}{2\sqrt{x}}-5x^4\right)\)
\(=3x^2\sqrt{x}+x^3\left(\dfrac{1}{2\sqrt{x}}-8x^4\right)\).
@2079957@
2. Hệ quả
- Hệ quả 1:
Nếu \(k\) là một hằng số thì \(\left(ku\right)'=ku'\).
- Hệ quả 2:
\(\left(\dfrac{1}{v}\right)'=-\dfrac{v'}{v^2}\left(v=v\left(x\right)\ne0\right)\).
Ví dụ 3: Tìm đạo hàm của hàm số \(y=\dfrac{1-2x}{x+3}\).
Giải:
Ta có: \(\left(\dfrac{1-2x}{x+3}\right)'=\dfrac{\left(1-2x\right)'\left(x+3\right)-\left(1-2x\right)\left(x+3\right)'}{\left(x+3\right)^2}\)
\(=\dfrac{-2\left(x+3\right)-\left(1-2x\right)}{\left(x+3\right)^2}\)
\(=-\dfrac{7}{\left(x+3\right)^2}\).
@2080477@
III. ĐẠO HÀM CỦA HÀM HỢP
1. Hàm hợp
Giả sử \(u=g\left(x\right)\) là hàm số của \(x\), xác định trên khoảng \(\left(a;b\right)\) và lấy giá trị trên khoảng \(\left(c;d\right)\); \(y=f\left(u\right)\) là hàm số của \(u\), xác định trên \(\left(c;d\right)\) và lấy giá trị trên \(R\). Khi đó ta lập một hàm số xác định trên \(\left(a;b\right)\) và lấy giá trị trên \(R\) theo quy tắc:
\(x\rightarrow f\left(g\left(x\right)\right)\)
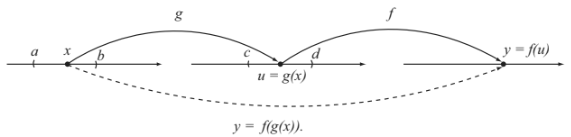
Ta gọi hàm số \(y=f\left(g\left(x\right)\right)\) là hàm hợp của hàm số \(y=f\left(u\right)\) và \(u=g\left(x\right)\).
Ví dụ 4: +) Hàm số \(y=\left(1-x^3\right)^{10}\) là hàm hợp của hàm số \(y=u^{10}\) và \(u=1-x^3\) ;
+) Hàm số \(y=\sin\left(\omega t+\gamma\right)\) là hàm hợp của hàm số \(y=\sin u\) với \(u=\omega t+\gamma\), trong đó \(\omega,\gamma\) là các hằng số ;
+) Hàm số \(y=\sqrt{x^2+x+1}\) là hàm hợp của hàm số \(y=\sqrt{u}\) và \(u=x^2+x+1\) ; ...
2. Đào hàm của hàm hợp
- Định lí 4:
Nếu hàm số \(u=g\left(x\right)\) các đạo hàm tại \(x\) là \(u'_x\) và hàm số \(y=f\left(u\right)\) có đạo hàm tại \(u\) là \(y'_u\) thì hàm hợp \(y=f\left(g\left(x\right)\right)\) có đạo hàm tại \(x\) là
\(y'_x=y'_u.u'_x\)
Ví dụ 5: Tính đạo hàm của hàm số \(y=\left(1-2x\right)^3\).
Giải:
Đặt \(u=1-2x\) thì \(y=u^3\) , \(y'_u=3u^2\) , \(u'_x=-2\)
Theo công thức tính đào hàm của hàm hợp ta có:
\(y'_x=y'_u.u'_x=3u^2.\left(-2\right)=-6u^2\)
Vậy \(y'_x=-6\left(1-2x\right)^2\).
Ví dụ 6: Tìm đạo hàm của hàm số \(y=\dfrac{5}{3x-4}\).
Giải:
Đặt \(u=3x-4\) thì \(y=\dfrac{5}{u}\) , \(y'_u=-\dfrac{5}{u^2}\) , \(u'_x=3\)
Theo công thức tính đào hàm của hàm hợp ta có:
\(y'_x=y'_u.u'_x=-\dfrac{5}{u^2}.3=-\dfrac{15}{u^2}=-\dfrac{15}{\left(3x-4\right)^2}\)
Vậy \(y'_x=-\dfrac{15}{\left(3x-4\right)^2}\).
@2079876@