§3. Hàm số bậc hai
Nội dung lý thuyết
Các phiên bản khácHàm số bậc hai được cho bởi công thức:
\(y=ax^2+bx+c\left(a\ne0\right)\)
Tập xác định của hàm số là: \(D=R\)
Hàm số \(y=ax^2\left(a\ne0\right)\) là một trường hợp riêng của hàm số này.
I. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI
1. Nhận xét
Xét đồ thị hàm số \(y=ax^2\left(a\ne0\right)\): Điểm \(O\left(0;0\right)\) là đỉnh của parabol \(y=ax^2\).
Đó là điểm thấp nhất của đồ thị trong trường hợp \(a>0\) (\(y\ge0\) với mọi \(x\)):
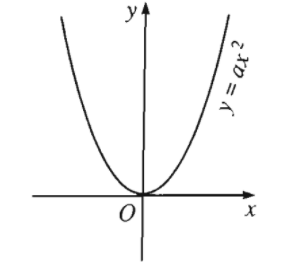
và là điểm cao nhất của đồ thị trong trường hợp \(a< 0\) (\(y\le0\) với mọi \(x\)):
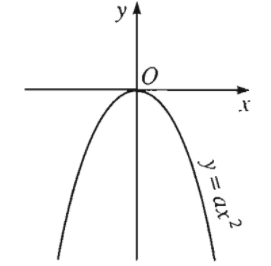
Ta có thể viết: \(y=ax^2+bx+c=a\left(x+\dfrac{b}{2a}\right)^2+\dfrac{-\Delta}{4a}\) với \(\Delta=b^2-4ac\)
Từ đó ta có nhận xét:
+) Điểm \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\) thuộc đồ thị hàm số \(y=ax^2+bx+c\left(a\ne0\right)\)
+) Nếu \(a>0\) thì \(y\ge\dfrac{-\Delta}{4a}\) với mọi \(x\), do đó \(I\) là điểm thấp nhất của đồ thị;
+) Nếu \(a< 0\) thì \(y\le\dfrac{-\Delta}{4a}\) với mọi \(x\), do đó \(I\) là điểm nhất của đồ thị.
Như vậy, điểm \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\) đối với đồ thị hàm số \(y=ax^2+bx+c\left(a\ne0\right)\) đóng vai trò như điểm \(O\left(0;0\right)\) của parabol \(y=ax^2\).
2. Đồ thị
Đồ thị của hàm số \(y=ax^2+bx+c\left(a\ne0\right)\) là một đường parabol có đỉnh là điểm \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\), có trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}\). Parabol này có bề lõm quay lên trên nếu \(a>0\), quay xuống dưới nếu \(a< 0\).
+) Với \(a>0\):
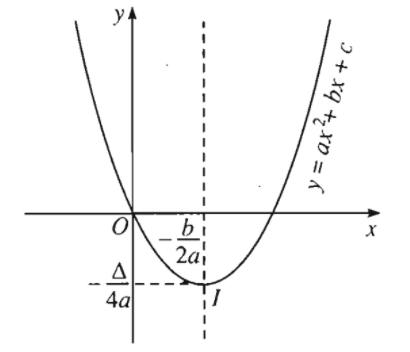
+) Với \(a< 0\):
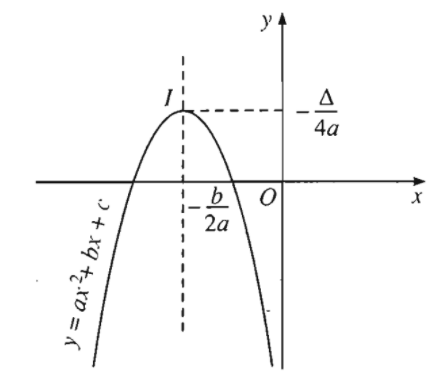
Ví dụ 1: Cho hàm số \(y=-x^2+5x-4\). Xác định tọa độ đỉnh của đồ thị hàm số.
Giải:
Xét hàm số \(y=-x^2+5x-4\) có:
\(\Delta=5^2-4.\left(-1\right).\left(-4\right)=9\) \(\Rightarrow\) \(-\dfrac{\Delta}{4a}=-\dfrac{9}{4.\left(-1\right)}=\dfrac{9}{4}\)
\(-\dfrac{b}{2a}=-\dfrac{5}{2.\left(-1\right)}=\dfrac{5}{2}\)
Do đó ta có: Đỉnh của parabol \(y=-x^2+5x-4\) là \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)=\left(\dfrac{5}{2};\dfrac{9}{4}\right)\)
@31409@
Ví dụ 2. Xác định trục đối xứng của parabol \(y=2x^2-3x+1\) và bề lõm của nó.
Giải:
Xét hàm số \(y=2x^2-3x+1\):
Do hệ số \(a=2>0\) nên parabol \(y=2x^2-3x+1\) có bề lõm quay lên trên.
Lại có: \(-\dfrac{b}{2a}=-\dfrac{-3}{2.2}=\dfrac{3}{4}\)
Vậy trục đối xứng của parabol \(y=2x^2-3x+1\) là \(x=\dfrac{3}{4}\).
@70534@
Ví dụ 3: Xác định phương trình của parabol có đỉnh \(I\left(\dfrac{1}{2};\dfrac{-5}{4}\right)\) và cắt trục tung tại điểm có tung độ bằng \(-1\).
Giải:
Gọi phương trình của parabol có dạng \(y=ax^2+bx+c\left(a\ne0\right)\)
Do parabol có đỉnh \(I\left(\dfrac{1}{2};\dfrac{-5}{4}\right)\)
Nên ta có: \(-\dfrac{b}{2a}=\dfrac{1}{2}\Rightarrow a=-b\) (1)
Lại có: \(-\dfrac{5}{4}=a.\left(\dfrac{1}{2}\right)^2+b.\left(\dfrac{1}{2}\right)+c\) \(\Rightarrow\) \(\dfrac{1}{4}a+\dfrac{1}{2}b+c=-\dfrac{5}{4}\) (2)
Mặt khác, parabol cắt trục tung tại điểm có tung độ bằng \(-1\)
\(\Rightarrow c=-1\) (3)
Từ (1), (2) và (3) ta có: \(\left\{{}\begin{matrix}a=-b\\\dfrac{1}{4}a+\dfrac{1}{2}b+c=-\dfrac{5}{4}\\c=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)
Vậy phương trình parabol cần tìm là \(y=x^2-x-1\).
3. Cách vẽ
Để vẽ đồ thị của hàm số \(y=ax^2+bx+c\left(a\ne0\right)\) ta thực hiện các bước làm sau:
+) Bước 1: Xác định tọa độ của đỉnh \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\) ;
+) Bước 2: Vẽ trục đối xứng \(x=-\dfrac{b}{2a}\) ;
+) Bước 3: Xác định tọa độ các giao điểm của parabol với trục tung (điểm \(\left(0;c\right)\)) và trục hoành (nếu có). Ta có thể xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm \(\left(0;c\right)\) qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn.
+) Bước 4: Vẽ parabol.
Khi vẽ parabol cần chú ý đến dấu của hệ số a (\(a>0\) bề lõm quay lên trên, \(a< 0\) bề lõm quay xuống dưới).
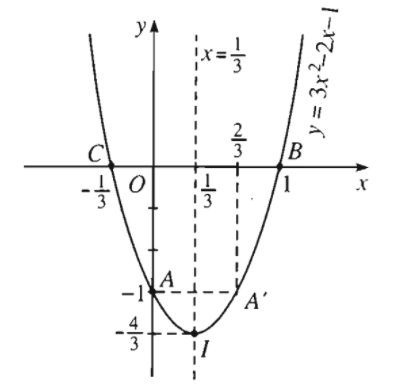
Ví dụ 1: Vẽ đồ thị hàm số \(y=3x^2-2x-1\).
Ta có:
+) \(\Delta=b^2-4ac=\left(-2\right)^2-4.3.\left(-1\right)=16\)
+) Đỉnh \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)=\left(\dfrac{1}{3};-\dfrac{4}{3}\right)\)
+) Trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}\) hay \(x=\dfrac{1}{3}\)
+) Giao điểm của đồ thị với trục tung là \(A\left(0;-1\right)\).
Điểm đối xứng với \(A\left(0;-1\right)\) qua trục đối xứng \(x=\dfrac{1}{3}\) là \(A'\left(\dfrac{2}{3};-1\right)\)
Giao điểm của parabol với trục hoành là \(B\left(1;0\right)\) và \(B'\left(-\dfrac{1}{3};0\right)\)
Từ đó, ta vẽ được parabol \(y=3x^2-2x-1\) như sau:
II. CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI
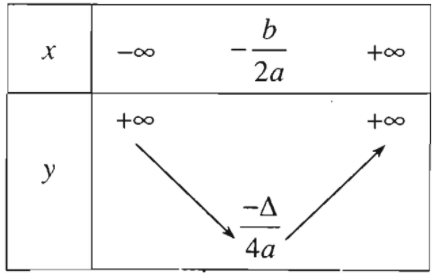
Ta có bảng biến thiên:
+) Với \(a>0\):
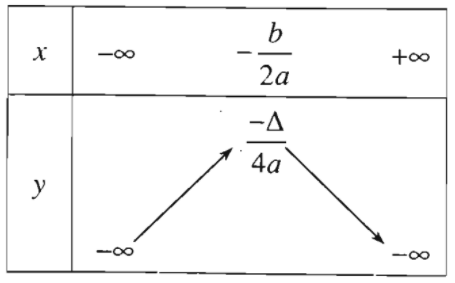
+) Với \(a< 0\):
Từ đó ta có định lí:
Nếu \(a>0\) thì hàm số \(y=ax^2+bx+c\)
Nghịch biến trên khoảng \(\left(-\infty;\dfrac{-b}{2a}\right)\) ;
Đồng biến trên khoảng \(\left(\dfrac{-b}{2a};+\infty\right)\).
Nếu \(a< 0\) thì hàm số \(y=ax^2+bx+c\)
Đồng biến trên khoảng \(\left(-\infty;\dfrac{-b}{2a}\right)\) ;
Nghịch biến trên khoảng \(\left(\dfrac{-b}{2a};+\infty\right)\).
Ví dụ 1: Xét hàm số \(y=-2x^2+x+3\):
Ta có: \(\dfrac{-b}{2a}=\dfrac{-1}{2.\left(-2\right)}=\dfrac{1}{4}\)
Do hệ số \(a=-2< 0\)
Nên hàm số \(y=-2x^2+x+3\) đồng biến trên khoảng \(\left(-\infty;\dfrac{1}{4}\right)\) và nghịch biến trên khoảng \(\left(\dfrac{1}{4};+\infty\right)\).
Ví dụ 2: Xét hàm số \(y=3x^2-2x+4\):
Ta có: \(\dfrac{-b}{2a}=\dfrac{-\left(-2\right)}{2.3}=\dfrac{1}{3}\)
Do hệ số \(a=3>0\)
Nên hàm số \(y=3x^2-2x+4\) nghịch biến trên khoảng \(\left(-\infty;\dfrac{1}{3}\right)\) và nghịch biến trên khoảng \(\left(\dfrac{1}{3};+\infty\right)\).
@70530@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Lê Thu Dương đã đóng góp một phiên bản khác cho bài học này (26 tháng 4 2021 lúc 17:36) | 0 lượt thích | |
| Giang Em-m đã đóng góp một phiên bản khác cho bài học này (17 tháng 4 2021 lúc 12:19) | 0 lượt thích |