Bài 3: Đường thẳng và mặt phẳng song song
Nội dung lý thuyết
Các phiên bản khácI. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
Cho đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\). Tuỳ theo số điẻm chung của \(d\) và \(\left(\alpha\right)\) ta có 3 trường hợp sau:

+) \(d\) và \(\left(\alpha\right)\) không có điểm chung. Khi đó ta nói \(d\) song song với \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) song song với \(d\) và kí hiệu là \(d\)//\(\left(\alpha\right)\) hay \(\left(\alpha\right)\)//\(d\).
+) \(d\) và \(\left(\alpha\right)\) có một điểm chung duy nhất \(M\). Khi đó ta nói \(d\) và \(\left(\alpha\right)\) cắt nhau tại điểm \(M\) và kí hiệu là \(d\cap\left(\alpha\right)=\left\{M\right\}\) hay \(d\cap\left(\alpha\right)=M\).
+) \(d\) và \(\left(\alpha\right)\) có từ hai điểm chung trở lên. Khi đó \(d\) nằm trong \(\left(\alpha\right)\) hay \(\left(\alpha\right)\) chứa \(d\) và kí hiệu là \(d\subset\left(\alpha\right)\) hay \(\left(\alpha\right)\supset d\).
@2142898@
II. TÍNH CHẤT
Định lí 1:
Nếu đường thẳng \(d\) không nằm trong mặt phẳng \(\left(\alpha\right)\) và \(d\) song song với đường thẳng \(d'\) nằm trong \(\left(\alpha\right)\) thì \(d\) song song với \(\left(\alpha\right)\).

Định lí 2:
Cho đường thẳng \(a\) song song với mặt phẳng \(\left(\alpha\right)\). Nếu mặt phẳng \(\left(\beta\right)\) chứa \(a\) và cắt \(\left(\alpha\right)\) theo giao tuyến \(b\) thì \(b\) song song với \(a\).

Ví dụ 1: Cho tứ diện \(ABCD\). Lấy \(M\) là điểm thuộc miền trong của tam giác \(ABC\). Gọi \(\left(\alpha\right)\) là mặt phẳng đi qua \(M\) và song song với các đường thẳng \(AB\) và \(CD\). Xác định thiết diện tạo bởi \(\left(\alpha\right)\) và tứ diện \(ABCD\). Thiết diện đó là hình gì?
Giải:

Mặt phẳng \(\left(\alpha\right)\) đi qua \(M\) và song song với \(AB\) nên \(\left(\alpha\right)\) cắt \(\left(ABC\right)\) theo giao tuyến \(d\) đi qua \(M\) và song song với \(AB\). Gọi \(E,F\) lần lượt là giao điểm của \(d\) với \(AC\) và \(BC\).
Mặt khác, \(\left(\alpha\right)\) song song với \(CD\) nên \(\left(\alpha\right)\) cắt \(\left(ACD\right)\) và \(\left(BCD\right)\) (là các mặt phẳng chứa \(CD\)) theo các giao tuyến \(EH\) và \(FG\) cùng song song với \(CD\) (\(H\in AD\) và \(G\in BD\))
Ta có thiết diện là tứ giác \(EFGH\).
Lại có \(\left(\alpha\right)\)//\(AB\), \(\left(ABD\right)\cap\left(\alpha\right)=HG\), từ đó suy ra \(HG\)//\(AB\).
Khi đó ta suy ra thiết diện \(EFGH\) là hình bình hành.
Hệ quả:
Nếu hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Hai đường thẳng chéo nhau thì không thể nằm trong cùng một mặt phẳng. Tuy nhiên ta có thể tìm được mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
@2142748@
Định lí 3:
Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Chứng minh:
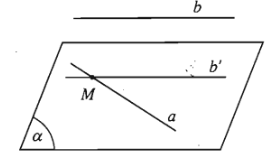
Giả sử ta có hai đường thẳng chéo nhau \(a\) và \(b\).
Lấy điểm \(M\) bất kì thuộc \(a\). Qua \(M\) kẻ đường thẳng \(b'\) song song với \(b\).
Gọi \(\left(\alpha\right)\) là mặt phẳng xác định bởi \(a\) và \(b'\).
Ta có \(b\)//\(b'\) và \(b'\subset\left(\alpha\right)\) từ đó suy ra \(b\)//\(\left(\alpha\right)\).
Hơn nữa \(\left(\alpha\right)\supset a\) nên \(\left(\alpha\right)\) là mặt phẳng cần tìm.
Ta chứng minh \(\left(\alpha\right)\) là duy nhất. Thật vậy, Nếu có một mặt phẳng \(\left(\beta\right)\) khác \(\left(\alpha\right)\), chứa \(a\) và song song với \(b\) thì khi đó \(\left(\alpha\right)\), \(\left(\beta\right)\) là hai mặt phẳng phân biệt cùng song song với \(b\) nên giao tuyến của chúng là \(a\), phải song song với \(b\). Điều này mâu thuẫn với giả thiết \(a\) và \(b\) chéo nhau.
Tương tự như vậy ta có thể chứng minh có duy nhất một mặt phẳng chứa \(b\) và song song với \(a\).
@2143487@