Bài 1. Điện tích. Định luật Cu-lông
Nội dung lý thuyết
Các phiên bản khácI. SỰ NHIỄM ĐIỆN CỦA CÁC VẬT. ĐIỆN TÍCH. TƯƠNG TÁC ĐIỆN
1. Sự nhiễm điện của các vật
Hiện tượng: Một thanh thủy tinh cọ xát với một miếng vải lụa hoặc một cây gậy cao su cứng với một miếng vải len, thì những vật đó có thể hút được những vật nhẹ như mẩu giấy, sợi bông. Ta nói thanh thủy tinh, hoặc cây gậy cao su đã bị nhiễm điện.
2. Điện tích. Điện tích điểm
● Vật bị nhiễm điện được gọi là vật mang điện, vật tích điện hay là một điện tích.
● Điện tích điểm là một vật tích điện có kích thước rất nhỏ so với khoảng cách tới điểm mà ta xét.
3. Tương tác điện. Hai loại điện tích
● Có 2 loại điện tích:
Điện tích dương (kí hiệu: + )
Điện tích âm (kí hiệu: - )
● Các điện tích cùng loại (dấu) thì đẩy nhau.
Các điện tích khác loại (dấu) thì hút nhau.
II. ĐỊNH LUẬT CU-LÔNG. HẰNG SỐ ĐIỆN MÔI
1. Định luật Cu-lông
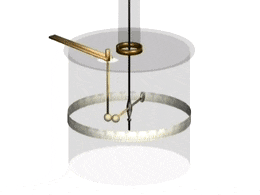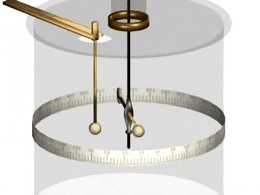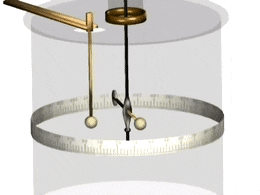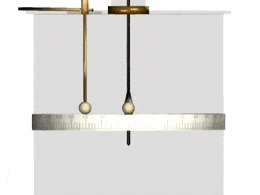
Cu-lông đã dùng một chiếc cân xoắn để đo lực đẩy giữa hai quả cầu nhỏ tích điện cùng dấu. Hai quả cầu nhỏ này được coi là những điện tích điểm.
Ông nhận thấy rằng, lực tương tác giữa hai quả cầu tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Mặt khác, chứng minh được lực tương tác giữa hai điện tích tỉ lệ thuận với tích độ lớn của hai điện tích đó.
Định luật Cu-lông
Lực hút hay đẩy giữa hai điện tích điểm đặt trong chân không có phương trùng với đường thẳng nối hai điện tích điểm đó, có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
\(F=k\dfrac{\left|q_1q_2\right|}{r^2}\)
Trong đó: F là lực tương tác giữa hai điện tích. Đơn vị: niutơn (N)
k là hệ số tỉ lệ, \(k = {9.10^9}\left( {\frac{{N.{m^2}}}{{{C^2}}}} \right)\)
q1, q2 là giá trị các điện tích. Đơn vị: cu - lông (C)
r là khoảng cách giữa 2 điện tích. Đơn vị: mét (m)
● Lực F - lực tương tác giữa 2 điện tích (lực tĩnh điện):
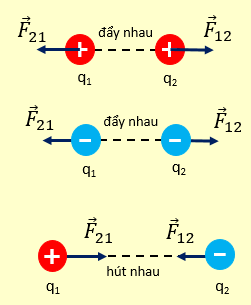
Phương: trùng với đường thẳng nối 2 điện tích
Chiều: thỏa mãn 2 điện tích cùng dấu thì đẩy nhau, 2 điện tích trái dấu thì hút nhau
Độ lớn: \(F=k\dfrac{\left|q_1q_2\right|}{r^2}\)
2. Lực tương tác giữa các điện tích điểm đặt trong điện môi đồng tính. Hằng số điện môi
● Điện môi là môi trường cách điện, ví dụ: dầu hỏa, giấy, thủy tinh,…
● Khi hai điện tích đặt trong điện môi thì lực tương tác giữa chúng giảm đi ε lần so với trong chân không, ε là hằng số điện môi.
Công thức của Định luật Cu-lông khi đó: \(F=k\dfrac{\left|q_1q_2\right|}{\varepsilon r^2}\)
3. Tổng hợp lực
● Một trong những bài toán vận dụng Định luật Cu-lông là ta cần phải tổng hợp hai hay nhiều lực cùng tác dụng lên một điện tích, vấn đề này ta đã được học trong chương trình lớp 10.
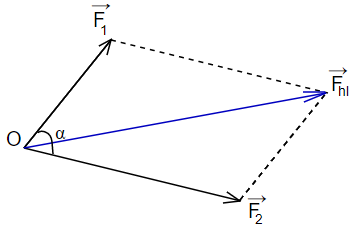
Hợp lực tác dụng lên điểm O: \({\overrightarrow F _{hl}} = {\overrightarrow F _1} + {\overrightarrow F _2}\)
Độ lớn: \(F_{hl}^2 = F_1^2 + F_2^2 + 2.{F_1}{F_2}\cos \alpha \)
Trường hợp đặc biệt:
\({\overrightarrow F _1} \uparrow \uparrow {\overrightarrow F _2}\) thì: \({F_{hl}} = {F_1} + {F_2}\)
\({\overrightarrow F _1} \uparrow \downarrow {\overrightarrow F _2}\) thì: \({F_{hl}} = \left| {{F_1} - {F_2}} \right|\)
\({\overrightarrow F _1} \bot {\overrightarrow F _2}\) thì: \({F_{hl}} = \sqrt {F_1^2 + F_2^2} \)
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn