Bài 3. Chuyển động thẳng biến đổi đều
Nội dung lý thuyết
Các phiên bản khácCHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
I. Vận tốc tức thời. Chuyển động thẳng biến đổi đều
1. Vận tốc thức thời
- Khái niệm: Là vận tốc của vật tại một thời điểm mà ta xét, vận tốc tức thời là đại lượng véc-tơ.
- Độ lớn của vận tốc tức thời: Trong khoảng thời gian rất ngắn \(\Delta t\), kể từ lúc ở M vật dời được một đoạn đường \(\Delta S\) rất ngắn thì
\(v =\dfrac{\Delta S}{\Delta t}\)
- Đơn vị: m/s
- Véc-tơ vận tốc tức thời \(\vec{v}\) có
- gốc đặt tại vật chuyển động
- hướng của chuyển động
- độ dài tỉ lệ với độ lớn của vận tốc tức thời theo một tỉ xích nào đó
2. Chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là chuyển động thẳng, trong đó vận tốc tức thời hoặc tăng dần đều hoặc giảm dần đều theo thời gian.
- Chuyển động có vận tốc tức thời tăng dần đều theo thời gian gọi là chuyển động nhanh dần đều.
- Chuyển động có vận tốc tức thời giảm dần đều theo thời gian gọi là chuyển động chậm dần đều.
II. Các đặc trưng trong chuyển động thẳng biến đổi đều
1. Gia tốc
- Gia tốc là đại lượng đặc trưng cho sự biến thiên nhanh chậm của vận tốc.
\(a =\dfrac{\Delta v}{\Delta t}\)
\(\Delta v = v -v_0\): độ biến thiên vận tốc
\(\Delta t = t - t_0\): độ biến thiên thời gian (thời gian chuyển động)
- Đơn vị: m/s2
- Véc tơ gia tốc
\(\vec a = \dfrac{\Delta \vec v}{\Delta t}\)
- Chuyển động nhanh dần đều \(\vec a\) cùng dấu với \(\vec{v_0}\)
- Chuyển động chậm dần đều \(\vec a\) ngược dấu với \(\vec{v_0}\)
2. Vận tốc của chuyển động thẳng biến đổi đều
- Công thức tính vận tốc
\(v = v_o + at\) (*)
\(v\) : vận tốc tại thời điểm t
\(v_0\) : vận tốc tại thời điểm ban đầu
- Đồ thị vận tốc – thời gian: vận tốc là hàm bậc nhất của thời gian nên đồ thị vận tốc - thời gian là một đường thẳng.
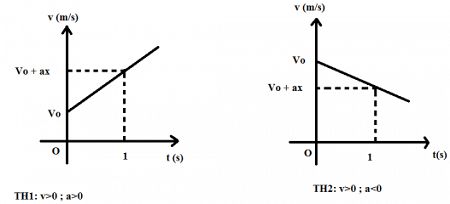
3. Quãng đường trong chuyển động thẳng biến đổi đều
\(S = v_0.t + \dfrac{1}{2}a.t^2\)
4. Phương trình chuyển động của chuyển động thẳng biến đổi đều
\(x = x_o + v_0.t + \dfrac{1}{2}.at^2\)
5. Công thức liên hệ giữa \(a\), \(v\) và \(S\) của chuyển động thẳng biến đổi đều (công thức độc lập thời gian)
\(v^2- v_0^2=2aS\)
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn