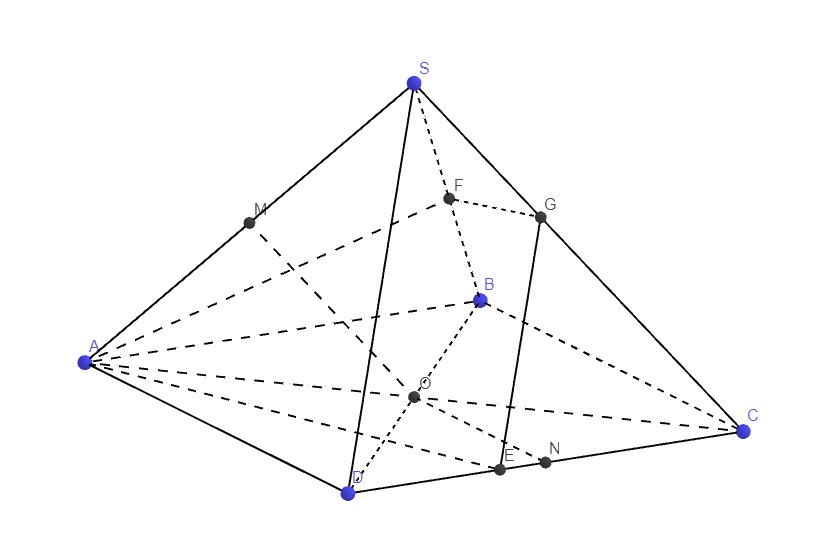
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
a) Chứng minh (OMN) // (SBC).
b) Giả sử hai tam giác SAD và ABC là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác ACD và SAB. Chứng minh EF // (SAD).
a.
O là trung điểm BD, N là trung điểm CD
\(\Rightarrow\) ON là đường trung bình tam giác BCD
\(\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\)
Tương tự ta có OM là đtb tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\)
\(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
Trong mp (SCD), qua E kẻ đường thẳng song song SD cắt SC tại G
\(\Rightarrow EG||SD\Rightarrow EG||\left(SAD\right)\) (1)
Theo định lý Talet: \(\dfrac{EC}{ED}=\dfrac{GC}{GS}\)
Mặt khác AE là phân giác của ACD nên theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\)
Mà ABC cân tại A \(\Rightarrow AB=AC\); SAD cân tại A \(\Rightarrow AD=SA\)
\(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\)
AF là phân giác nên áp dụng định lý phân giác:
\(\dfrac{FB}{FS}=\dfrac{AB}{SA}\) \(\Rightarrow\dfrac{FB}{FS}=\dfrac{GC}{GS}\Rightarrow FG||BC\) (Talet đảo)
\(\Rightarrow FG||AD\Rightarrow FG||\left(SAD\right)\) (2)
(1);(2) \(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||\left(SAD\right)\)
Cho hình chóp S.ABCD có đáy là hình bình hành. Lấy điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}+\overrightarrow{MS}=\overrightarrow{0}\) . Mặt phẳng đi qua AM cắt SB, SC, SD thứ tự tại B' C' D'. Tính \(\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}\)
Gọi O là giao điểm AC và BD, theo t/c hình bình hành \(\Rightarrow O\) là trung điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\\\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\end{matrix}\right.\)
Từ giả thiết:
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}+\overrightarrow{MS}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}+\overrightarrow{MO}+\overrightarrow{OS}=\overrightarrow{0}\)
\(\Leftrightarrow5.\overrightarrow{MO}+\overrightarrow{OS}=0\)
\(\Leftrightarrow\overrightarrow{OM}=\dfrac{1}{5}\overrightarrow{OS}\)
Hay M là điểm thuộc đoạn thẳng OS sao cho \(OM=\dfrac{1}{5}OS\) \(\Rightarrow SM=4MO\)
Do M thuộc OS \(\Rightarrow M\in\left(SAC\right)\), kéo dài AM cắt SC tại \(C'\) \(\Rightarrow C'\) là điểm cố định (bất chấp vị trí mặt phẳng (P))
Áp dụng định lý Menelaus trong tam giác SOC với 3 điểm A, M, C' thẳng hàng:
\(\dfrac{MS}{MO}.\dfrac{OA}{AC}.\dfrac{CC'}{C'S}=1\Rightarrow4.\dfrac{1}{2}.\dfrac{CC'}{C'S}=1\Rightarrow\dfrac{CC'}{SC'}=\dfrac{1}{2}\)
Bây giờ tới B' và D'.
Cách đơn giản nhất là đề ko cho biết rõ về mp (P), nó chỉ cần chứa AM là đủ, do đó ta chọn vị trí đơn giản nhất của (P) để tính, đó là (P) song song BD. Khi đó, qua M kẻ đường thẳng song song BD lần lượt cắt SB, SD tại B' và D'
Theo định lý Talet:
\(\dfrac{BB'}{SB'}=\dfrac{DD'}{SD'}=\dfrac{MO}{SM}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}=\dfrac{1}{4}+\dfrac{1}{2}+\dfrac{1}{4}=1\)
Trong trường hợp ko muốn làm kiểu chọn mp đặc biệt này thì ta có thể chọn vị trí bất kì cho B', nhưng sẽ tốn thời gian hơn nhiều. Nếu em cần thì cũng có thể giải quyết theo cách ấy.
Tổng quát:
Trước hết ta nhắc lại định lý đồng phẳng: cho 3 vecto \(\overrightarrow{a};\overrightarrow{b};\overrightarrow{c}\), chúng đồng phẳng khi và chỉ khi tồn tại các số thực m; n sao cho \(\overrightarrow{a}=m.\overrightarrow{b}+n.\overrightarrow{c}\) (1)
Bây giờ ta dựa vào đó chứng minh định lý khác về đồng phẳng trong không gian:
4 điểm A;B;C;D đồng phẳng khi \(\overrightarrow{SD}=p.\overrightarrow{SA}+m.\overrightarrow{SB}+n.\overrightarrow{SC}\) với 1 điểm S là 1 điểm bất kì và \(m;n;p\) là các số thực thỏa mãn \(m+n+p=1\)
C/m: do A;B;C;D đồng phẳng \(\Rightarrow\overrightarrow{AB};\overrightarrow{AC};\overrightarrow{AD}\) đồng phẳng
Theo (1), tồn tại các số thực m và n sao cho:
\(\overrightarrow{AD}=m.\overrightarrow{AB}+n.\overrightarrow{AC}\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}=m\left(\overrightarrow{AS}+\overrightarrow{SB}\right)+n\left(\overrightarrow{AS}+\overrightarrow{SC}\right)\)
\(\Leftrightarrow\overrightarrow{SD}=m.\overrightarrow{SB}+n.\overrightarrow{SC}+\left(1-m-n\right).\overrightarrow{SA}\)
Đặt \(1-m-n=p\Rightarrow\left\{{}\begin{matrix}m+n+p=1\\\overrightarrow{SD}=m.\overrightarrow{SB}+n.\overrightarrow{SC}+p.\overrightarrow{SA}\end{matrix}\right.\) (đpcm)
Quay lại bài toán, ta tính toán cho trường hợp các điểm B' D' lần lượt nằm trên đoạn thẳng SB và SD (trường hợp có 1 điểm nằm ngoài tính y hệt).
Đặt \(\dfrac{SB}{SB'}=x;\dfrac{SC}{SC'}=y;\dfrac{SD}{SD'}=z\)
Do O là trung điểm AC và BD nên: \(\left\{{}\begin{matrix}\overrightarrow{SA}+\overrightarrow{SC}=2\overrightarrow{SO}\\\overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=4\overrightarrow{SO}\)
\(\Rightarrow\overrightarrow{SA}+x.\overrightarrow{SB'}+y.\overrightarrow{SC'}+z.\overrightarrow{SD'}=5\overrightarrow{SM}\) (do \(\overrightarrow{SO}=\dfrac{5}{4}\overrightarrow{SM}\))
Do A;B'C'D' đồng phẳng nên tồn tại \(m+n+p=1\) sao cho \(\overrightarrow{SA}=m.\overrightarrow{SB'}+n.\overrightarrow{SC'}+p.\overrightarrow{SD'}\)
\(\Rightarrow\left(m+x\right)\overrightarrow{SB'}+\left(n+y\right)\overrightarrow{SC'}+\left(p+z\right)\overrightarrow{SD'}=5\overrightarrow{SM}\)
\(\Leftrightarrow\overrightarrow{SM}=\dfrac{1}{5}\left(m+x\right)\overrightarrow{SB'}+\dfrac{1}{5}\left(n+y\right)\overrightarrow{SC'}+\dfrac{1}{5}\left(p+z\right)\overrightarrow{SD'}\)
Do M;B'C'D' đồng phẳng nên:
\(\dfrac{1}{5}\left(m+x\right)+\dfrac{1}{5}\left(n+y\right)+\dfrac{1}{5}\left(p+z\right)=1\)
\(\Leftrightarrow m+n+p+x+y+z=5\)
\(\Leftrightarrow1+x+y+z=5\)
\(\Leftrightarrow x+y+z=4\)
\(\Leftrightarrow\dfrac{SB}{SB'}+\dfrac{SC}{SC'}+\dfrac{SD}{SD'}=4\)
\(\Leftrightarrow\dfrac{SB'+BB'}{SB'}+\dfrac{SC'+CC'}{SC'}+\dfrac{SD'+DD'}{SD'}=4\)
\(\Leftrightarrow\dfrac{BB'}{SB'}+\dfrac{CC'}{SC'}+\dfrac{DD'}{SD'}=1\)
Cho tứ diện đều ABCD Cạnh a. Gọi G là trọng tâm △ABD, điểm M,H lần lượt thuộc cạnh CD, AD sao cho DM=2MC, DH=2HA. Gọi E là giao điểm DG và BH. Mặt phẳng (α) đi qua E song song (ABC) cắt BM tại F. Tính EF ?
Sợi dây AB dài 170 cm có dầu A gắn vào nguồn sóng, đầu B thả tự do. Khi đầu A gắ một máy phát tần số có thể thay đổi. Ban đầu điều chính để máy phát tần số dao động với tần số 100 trên dây có sóng dùng với 9 bụng sóng
a) Tìm bước sóng, tốc độ truyền sóng.
b) Nếu tăng tần số từ 100 Hz đến 225 Hz thì có mấy lần sóng dừng xuất hiện trên sợi dây?
Đồ thị li độ, vận tốc, gia tốc theo thời gian có dạng hình gì?
chứng minh rằng pt: \(\left(1-m\right)x^5+9mx^2-16x-m=0\) có ít nhất 2 nghiệm pb với mọi giá trị của m
Dễ thấy hàm \(f\left(x\right)=\left(1-m\right)x^5+9mx^2-16x-m\) liên tục trên R với mọi giá trị của m
Ta có:
\(f\left(-2\right)=\left(1-m\right).\left(-2\right)^5+9m.\left(-2\right)^2-16.\left(-2\right)-m\)
\(=-32\left(1-m\right)+4.9m+32-m=67m\)
\(f\left(0\right)=-m\)
\(f\left(2\right)=\left(1-m\right).2^5+9m.2^2-16.2-m\)
\(=32\left(1-m\right)+4.9m-32-m=3m\)
Nếu \(m=0\) thì ta có đpcm
Nếu \(m\ne0\) thì
\(\left\{{}\begin{matrix}f\left(-2\right).f\left(0\right)=-67m^2< 0\\f\left(0\right).f\left(2\right)=-3m^2< 0\end{matrix}\right.\)
Do đó pt đã cho có ít nhất một nghiệm trên mỗi khoảng \(\left(-2;0\right)\) và \(\left(0;2\right)\)
\(\Rightarrowđpcm\)
Vậy ta có điều phải chứng minh
Ở đây cần chọn \(x\) sao cho \(x^5-16x=0\) để khi thay vào \(f\left(x\right)\) sẽ không còn hệ số tự do mà chỉ có \(m\) để dễ đánh giá
Vì lí do đó nên ta chọn được \(x=0;x=-2;x=2\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H, I, K lần lượt là trung điểm của SA, SB, SC, M là giao điểm của AI và KD, N là giao điểm của DH và CI.
a) Chứng minh rằng SM // (ABCD).
b). Chứng minh rằng (SMN)/(ABCD).
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình bình hành. Lấy một điểm \(M\) thuộc cạnh \(SC\). Mặt phẳng \(\left(ABM\right)\) cắt \(SC\) tại điểm \(N\). Chứng minh \(NM\) song song với \(CD\).
Cầu xin các bạn giúp mình với ạ 
Giúp em bài tập về nhà với ạ. Em cảm ơn ạ
a: \(N\in SB\subset\left(SBC\right)\)
\(N\in\left(NAD\right)\)
Do đó: \(N\in\left(SBC\right)\cap\left(NAD\right)\)
Xét (SBC) và (NAD) có
\(N\in\left(SBC\right)\cap\left(NAD\right)\)
BC//AD
Do đó: (SBC) giao (NAD)=xy, xy đi qua N và xy//BC//AD
b: Trong mp(ABCD), Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\left(1\right)\)
\(S\in SA\subset\left(SAC\right)\)
\(S\in SB\subset\left(SBD\right)\)
Do đó: \(S\in\left(SAC\right)\cap\left(SBD\right)\left(2\right)\)
Từ (1) và (2) suy ra (SAC) giao (SBD)=SO
c: Chọn mp(SBC) có chứa NK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SCA\right)\)
Do đó: \(\left(SBC\right)\cap\left(SCA\right)=SC\)
Gọi E là giao điểm của NK với SC
=>E là giao điểm của NK với mp(SAC)
d: Chọn mp(SBD) có chứa DN
Ta có: (SBD) giao (SAC)=SO(cmt)
nên ta sẽ gọi F là giao điểm của SO với DN
=>F là giao điểm của ND với mp(SAC)
e: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình của ΔSAB
=>MN//AB và \(MN=\dfrac{AB}{2}\)
MN//AB
AB//CD
Do đó: MN//CD
Xét tứ giác MNCD có MN//CD
nên MNCD là hình thang
